



Next: Big-O Notation and Algorithm
Up: Weiss Chapter 2 Notes
Previous: Definitions
Although the definitions given above completely define what the big-O
of a function is, it is not always immediately obvious how to use them
to actually discover the big-O of a function. Finding the order of
many useful functions can be a challenging task, and there are even
functions that have defied all attempts at a complete analysis!
Luckily, since there has been so much work done in the area already,
finding the big-O of many functions is simply a matter of finding a
known result for a similar function and using it.
The following rules provide a jumping off point:
- If
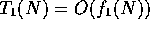 and
and  ,
then:
,
then:
-
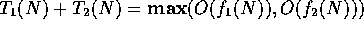
-
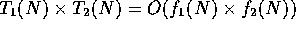
- If T(N) is a polynomial of degree k, then
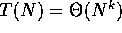 .
.
The fact that 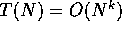 follows from the previous
rule. Showing that
follows from the previous
rule. Showing that 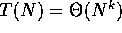 is slightly more
complicated, but can be proven by showing that there is always
a choice of c and
is slightly more
complicated, but can be proven by showing that there is always
a choice of c and  that satisfies the definition of
that satisfies the definition of
 .
.
-
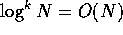 , for any constant k.
, for any constant k.
This is true, but of relatively limited use. Since O(N) is
an upper bound, it is OK to say that anything with a lower
order is O(N). This is handy as a last resort, when trying
to find the big-O of a nasty function that includes
logarithms, but whenever possible it is useful to draw a
distinction between O(N) and 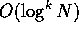 . For example,
an algorithm that has a big-O of
. For example,
an algorithm that has a big-O of 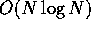 is (usually)
much better than an algorithm that is
is (usually)
much better than an algorithm that is  .
.
Another method of finding the big-O of a function is to find the
dominant term of the function, and find its order. The order
of the dominant term will also be the order of the function.
The dominant term is the term that grows most quickly as n becomes
large. Some rules of dominance include the following:
- Any exponential function of n dominates any polynomial
function of n.
- Any polynomial function of n dominates any logarithmic
function of n.
- Any logarithmic function of n dominates a constant term.
- A polynomial of degree k dominates a polynomial of degree l
if and only if k > l.
There are additional rules that you can discover for yourself. The
key is that term x(n) dominates function y(n) if and only if
x(n)/y(n) grows as n grows large.
Using these rules can sometimes make finding the order of a
complicated function easy. For example, the function
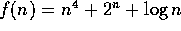 , is clumsy to manipulate algebraically.
However, thanks to the rules of dominance, we know that we
the
, is clumsy to manipulate algebraically.
However, thanks to the rules of dominance, we know that we
the 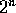 term will dominate the order of this function, so
we can simply find the order of
term will dominate the order of this function, so
we can simply find the order of 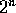 , which is itself. Therefore,
we can immediately say that
, which is itself. Therefore,
we can immediately say that 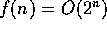 .
.
There are other methods that can be used find the order of functions.
but we will not introduce them yet. Later in the semester, when we
analyze several recursive algorithms, methods for analyzing the order
of recursive functions will be introduced.
Since the orders of functions look like ordinary functions, it is
tempting to treat them as such, and manipulate them as though they
were ordinary functions. This is usually a huge mistake.
For example, let  and
and 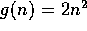 . It should be clear
that the both f(n) and g(n) are
. It should be clear
that the both f(n) and g(n) are 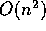 . What is the
big-O of g(n) - f(n)? If we compute the order of the difference
as the difference of the orders, then we would mistakenly conclude
that (g(n) - f(n)) = the order of f(n) less the order of g(n),
or
. What is the
big-O of g(n) - f(n)? If we compute the order of the difference
as the difference of the orders, then we would mistakenly conclude
that (g(n) - f(n)) = the order of f(n) less the order of g(n),
or 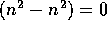 . This answer is obviously wrong.
If we actually compute g(n) - f(n), however, we arrive at the correct
conclusion:
. This answer is obviously wrong.
If we actually compute g(n) - f(n), however, we arrive at the correct
conclusion: 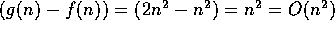 .
.




Next: Big-O Notation and Algorithm
Up: Weiss Chapter 2 Notes
Previous: Definitions
Dan Ellard
Mon Jul 21 22:30:59 EDT 1997
![]() follows from the previous
rule. Showing that
follows from the previous
rule. Showing that ![]() is slightly more
complicated, but can be proven by showing that there is always
a choice of c and
is slightly more
complicated, but can be proven by showing that there is always
a choice of c and ![]() that satisfies the definition of
that satisfies the definition of
![]() .
.
![]() . For example,
an algorithm that has a big-O of
. For example,
an algorithm that has a big-O of ![]() is (usually)
much better than an algorithm that is
is (usually)
much better than an algorithm that is ![]() .
.