



Next: Finding the Big-O of
Up: Weiss Chapter 2 Notes
Previous: Weiss Chapter 2 Notes
The order of a function T(N) is a description of its rate of
growth as N becomes very large.
When analyzing the order of algorithms, the following definitions are
commonly used:
- T(N) = O(f(N))
if there are positive constants c and
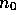 such that
such that 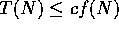 when
when 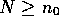 .
.
As an example, if T(N) = 2N + 1, then T(N) = O(N).
To prove this, all we need to do is find c and 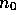 such that
such that 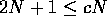 when
when 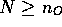 . If
we try c = 3, then we can subtract 2N from both
sides of the inequality and get
. If
we try c = 3, then we can subtract 2N from both
sides of the inequality and get 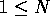 . This
is clearly true when
. This
is clearly true when 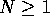 , so
, so 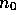 is 1.
is 1.
It may seem strange that in this case f(N) is
clearly less than T(N) for all positive values
of N, and yet T(N) = O(f(N)). The actual values
of T(N) and f(N) are not the issue- the important
issue is whether a c and 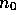 can be found that
satisfy this rule.
can be found that
satisfy this rule.
-
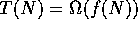 if there are positive constants c and
if there are positive constants c and 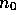 such that
such that 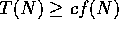 when
when 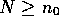 .
.
This is similar to the big-O notation, but from the other
direction- the order of f(N) is typically as large as
possible without making it larger than the order of T(N).
As an example, if T(N) = 2N + 1, then T(N) = O(N). To
prove this, once again all we need to do is find c and 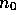 such that
such that 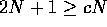 when
when 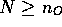 . If we try c =
2, then we can subtract 2N from both sides of the
inequality and get
. If we try c =
2, then we can subtract 2N from both sides of the
inequality and get 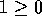 . This is clearly true for any
N.
. This is clearly true for any
N.
-
 if and only if T(N) = O(f(N)) and
if and only if T(N) = O(f(N)) and 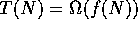 .
.
- T(N) = o(f(N))
if and only if T(N) = O(f(N)) and
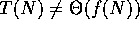 .
.
Remember that in this notation, our goal is to find f(N) (an order),
given T(N) (a function). For example, imagine that we have a
function 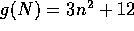 , and we would like to say things about it
using big-O notation. It is correct to say ``g(N) is
, and we would like to say things about it
using big-O notation. It is correct to say ``g(N) is 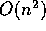 '' but
it is usually not correct to say ``O(g(N)) is
'' but
it is usually not correct to say ``O(g(N)) is 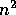 ''.
''.
It may seem strange that the order of f(N) might actually be
greater than the order of T(N). For example, if 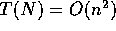 ,
then it is also true that
,
then it is also true that 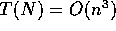 , and so on.
, and so on.
By general convention, f(N) is chosen to be the smallest order that
is known to be greater or equal to the order of T(N). In this
example, you would never say that 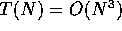 if you knew that
if you knew that
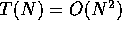 . It would be correct, at least in a mathematical sense,
but potentially very misleading to the reader. In fact, in many
contexts, big-O is used synonymously with big-theta.
. It would be correct, at least in a mathematical sense,
but potentially very misleading to the reader. In fact, in many
contexts, big-O is used synonymously with big-theta.
As another convention, any constant factors are dropped from the
order. For example, according to the definition given above, it is
true that 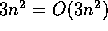 . However, it is also true that
. However, it is also true that  . The latter form, where the constant factor has been
omitted, is the standard way of expressing the big-O of a function.
. The latter form, where the constant factor has been
omitted, is the standard way of expressing the big-O of a function.
Similarly, it is also a convention to drop all but the ``largest''
term of the order. The largest term is the dominant term (see
section 2.2.1 for more information). For example, 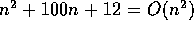 , since as n becomes large, the quadratic term
will grow more quickly than the others.
, since as n becomes large, the quadratic term
will grow more quickly than the others.
At first glance, it would appear that  is all we really want
or need- after all, it's the ``right'' answer, where the order of
T(N) is exactly f(N). If we know the real order of T(N), then
we know
is all we really want
or need- after all, it's the ``right'' answer, where the order of
T(N) is exactly f(N). If we know the real order of T(N), then
we know 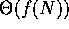 .
.
Unfortunately, life is not so simple. Consider the following code
snippet:
1 void strange1 (int A[N])
2 {
3 int i;
4
5 for (i = 0; i < N; i++) {
6 if (A[N] == 0) {
7 break;
8 }
9 printf ("A [%d] = %d\n", i, A[i]);
10 }
11 }
What is the order of strange1? It is impossible to know without
knowing what the contents of array A are: if there is always a
zero element in the array, and the first zero element is always at a
fixed location in this array (for example, the first location), then
this function is 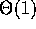 - it always takes the same amount of time
to run, regardless of N. If we know that there isn't a zero
element anywhere in the array, then this algorithm is
- it always takes the same amount of time
to run, regardless of N. If we know that there isn't a zero
element anywhere in the array, then this algorithm is 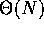 ,
since it visits every location in the array, and the array is of
length N. If we don't know anything about the contents of the
array, however, then we can't be sure what the order is, so we don't
know what the true order of
,
since it visits every location in the array, and the array is of
length N. If we don't know anything about the contents of the
array, however, then we can't be sure what the order is, so we don't
know what the true order of 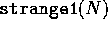 is. We know that the
order is no less than order 1, so
is. We know that the
order is no less than order 1, so 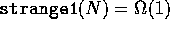 . Similarly, we know that the order is no larger than
N, so
. Similarly, we know that the order is no larger than
N, so 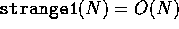 .
.




Next: Finding the Big-O of
Up: Weiss Chapter 2 Notes
Previous: Weiss Chapter 2 Notes
Dan Ellard
Mon Jul 21 22:30:59 EDT 1997
![]() such that
such that ![]() when
when ![]() . If
we try c = 3, then we can subtract 2N from both
sides of the inequality and get
. If
we try c = 3, then we can subtract 2N from both
sides of the inequality and get ![]() . This
is clearly true when
. This
is clearly true when ![]() , so
, so ![]() is 1.
is 1.
![]() can be found that
satisfy this rule.
can be found that
satisfy this rule.
![]() such that
such that ![]() when
when ![]() . If we try c =
2, then we can subtract 2N from both sides of the
inequality and get
. If we try c =
2, then we can subtract 2N from both sides of the
inequality and get ![]() . This is clearly true for any
N.
. This is clearly true for any
N.