S-Q 1997 - Assignment 3 Due 07/17/97 at 6:00pm Last Date Accepted: 07/21/97 at 6:00pm

Getting Prepared

1. Copy over the files for this assignment. Copy all of the files from libsq/assts/asst3 into your directory /Q/asst3 (which should have been created when you ran q-setup for assignment 1).

Exercises (100 points)

All work should be done in directory /Q/asst3. The Makefile provided includes rules to build all the programs in this assignment; you shouldn't need to change it at all. If you add additional files for your animals program, then you may need to add these files to the Makefile; see the Makefile for directions.

1. (5 points) Show the patricia that would result from adding the keys ``banana'', ``bandana'', ``bandolero'', ``biscuit'', ``bisection'', ``ban'', ``bisect'', and ``banner'' to an empty patricia. You do not have to draw the tree after each insertion; just show the final tree.

   Hand-drawn figures are preferable; do not spend a lot of time trying to make the figures beautiful.

2. (5 points) Draw the 2-3 trees that would result from inserting the following keys into an empty 2-3 tree, in the following order: A D B G C H E F. Draw the tree after each insertion.

   Once again, hand-drawn figures are preferable.

3. (5 points) Prove that the search for a key in a de la Briandais trie is O(l) (where l is the length of the key) regardless of the number of keys in the trie, even though the lengths of the linked lists traversed during the search may depend on the number of keys.

   You can write out your proof longhand or use whatever tools you wish to edit it. If you use plaintext, place your answer in file asst3.txt.

4. (20 points) Devise an algorithm that prints the keys in a binary tree in level-order, as described in Weiss, section 4.6. Hint- use a queue.

   A level-order traversal processes the root node, then the keys of the nodes at depth 1 (from left to right), then the keys of the nodes at depth 2 (again from left to right), and so on. The traversal must run in time O(n) and space O(n), where n is the number of nodes in the tree (regardless of the shape of the tree).

   You can write out your algorithm longhand or use whatever tools you wish to edit it. If you use plaintext, place your answer in file asst3.txt.

   You do not need to implement your algorithm, but your algorithm should be detailed enough that it would be easy to implement.

5. (25 points) Complete all of the functions in tree_utils.c. The functions in tree.c are provided as helper functions, and tree_test.c is a simple test driver which you may modify in any way you see fit as you test your functions.
6. (40 points) Implement the game of animals by implementing function play_animals in file animals.c.

   An animal tree is a binary tree where the internal nodes are called question nodes and represent questions, while the leaves are called animal nodes and represent the names of animals. The questions are always yes/no questions. All the left descendants of a question nodes correspond to a ``yes'' answer and all the right descendants a ``no'' answer. The game of animals is an interactive program that constructs an animal tree, based on input from the user, and uses this information to try to guess the identity of whatever animal the user thinks of.

   Figure shows an example dialog with the game, produced by sol_animals. (You may find it very useful to run sol_animals to get a feel for how your program should work. Do not feel compelled to provide a completely identical user interface, but do make sure that your program is easy to use and has a sensible user interface.) Figure shows the corresponding animal tree that would exist at the end of the game illustrated in figure , and figure shows how this tree looks as each new animal and question is added.

   Many functions that you may find useful are already implemented in animals.c (with corresponding declarations and definitions in animals.h. You may use, modify, or ignore this code in any way you wish.

Graduate Problem (25 points)

As mentioned in lecture, is possible to traverse a binary tree iteratively, without any use of recursion. Complete function treePrintIterative in tree_print.c so that it is functionally identical to treePrintRecursive, but does not use recursion at all. For full credit, your algorithm must run in time O(n) and space O(n), where is n is the number of nodes in the tree. Be sure to document your algorithm; a reasonable algorithm is worth many points, even if the code is not perfect.

Hint- you may find a stack very useful. You may also notice some similarity between this algorithm and your algorithm for performing a level-order traversal- in particular, the code to perform a preorder traversal using a stack may remind you of your algorithm for performing a level-order traversal using a queue. Implementing inorder and postorder traversals requires an additional trick, however.

Submit Your Work

1. Use the submit program to hand in your work. From your directory /Q, run the submit program. The name of the course is cscisq, and the name of the project is asst3, and the name of the file to submit is also asst3. (See the UNIX tutorial for more info about submit.)
2. Print out and hand in a copy of your animals.c (and any other files you modified or created to implement animals), asst3.txt, tree_utils.c, and your drawings for the written problems. Graduate students should also hand in a printout of their tree_print.c.

 
Figure:   The text of a short game of animals. User input is indicated by a bold font.

 
Figure:   An animal tree.

 
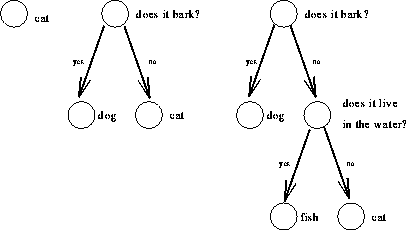
Figure:   Construction of the animal tree.

About this document ...

This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 asst3.tex.

The translation was initiated by Dan Ellard on Thu Jul 10 12:03:09 EDT 1997