Exercises

1. Prove the statement (from section 6.3.2) that it is always possible that the escape character can be used to escape itself (assuming that the delimiting character is different from the escape character).
2. Our method of reading a binary search tree is , since it inserts n items into the tree, with an expected time of per insertion. (In the worst case, of course, each insertion may be O(n), so that the reconstruction requires time 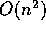). This is not usually a matter of concern, since the O(n) disk operations necessary will be so much slower than the tree insertion. For very large and unbalanced trees, however, this could present a problem.

   Show how it is possible, by storing an additional O(n) items of data with the tree (and using O(n) additional memory while the tree is being reconstructed) to always reconstruct the tree in time O(n). (If you find a way achieve time O(n) with less then O(n) additional storage, feel free to explain how this can be accomplished- but be careful!)

   Hint- consider the techniques for storing unordered binary trees.

3. Show how it is possible to use the idea behind algorithms 6.2 and 6.3 so that unordered trees can be written and read using the basic ideas behind these algorithms but without modifying the original tree or marking any of its nodes in any way. O(n) extra storage space can be used (both in the file and in memory).