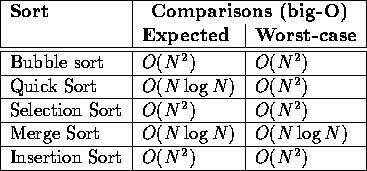
5, 4, 3, 1, 2, 0, 6
See attached sheet.
,
draw the hash tables that would result from inserting the keys
0, 1, 13, 2, 3, 7 into initially empty hash tables
(of size 7) with the following characteristics:
- Open addressing with linear probing.
See attached sheet.
- Separate chaining.
See attached sheet.
double i, j;
int M = 0, N = 0;
for (i = 0.0; i < 1.0; i += 0.1) {
for (j = 0.0; j < 1.0; j += 0.1) {
N++;
if (inside (i, j)) {
M++;
}
}
}
return ((double) M / N);
Your coworker Sam thinks that Chris's method is not good, and will fail for many shapes. Who is correct? Convince the other. Briefly explain your reasoning.
Sam is correct. Chris's method will not work well for many shapes.
For example, if the shape consists of a bunch of dots arranged so that each dot falls under one of Chris's sample positions, then the reported area can be very high (an estimate of 1.0, if all of the sample points have a corresponding dot) even though the true total area of the dots may be very close to 0.0.
Conversely, if the shape consists of a large square perforated by holes that fall under Chris's sample points, then the estimate of the area can be 0.0 while the true area is nearly 1.0.
For any fixed sampling strategy, there exist shapes that give utterly inaccurate estimates, and these shapes are easy to construct. A devious caller can easily tailor their shapes to achieve any estimate they desired, if an algorithm of this kind was used.
The defense against this is to use the Monte Carlo method. The accuracy of the estimate given by the Monte Carlo method is unrelated to the actual shape whose area is being estimated- the area of the shape is all that matters. The accuracy of the estimate depends entirely on the number of samples taken. A devious caller cannot subvert the Monte Carlo algorithm by choosing a particular shape- all they can do is hope that the random number generator happens to work in their favor.
A less obvious problem with Chris's algorithm is that we don't have a good way of measuring how accurate our result is, for any given shape. We know that our estimate might be completely wrong (if one of the bad shapes is used), but how accurate should we expect it to be, in general, for a randomly chosen shape? Some people guessed that the margin of error and confidence level equations for the Monte Carlo estimates would hold here- but this is not the case. Those equations assume that the samples are random and independent, while Chris's method of sampling is neither. (There is a way of estimating the expected accuracy of the estimate generated by Chris's algorithm, averaged over all possible shapes- but this is of little use when presented with a single shape to estimate.
Some people postulated that Chris's algorithm would work better if more samples were taken. This is true for many shapes, but not for all. We know that the margin of error at any confidence level will shrink as we take more samples if we use Monte Carlo, but we don't have an way to know if the same is true with Chris's method.
Pattern = EDGED
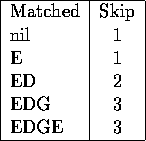
Pattern = S Y N T A X
Text = T H I S E X A M I S N O T A B O U T S Y N T A X
See attached sheet.
