- Weiss, 1.10.
- Prove that
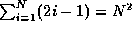 .
.
First, prove the base case. For N=1, this
is easy to show:
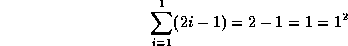
Now prove the induction; prove that if this
relationship holds for any N, then it also holds for
N+1.
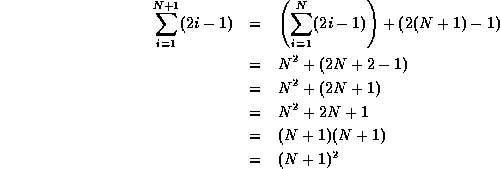
- (10 points) Weiss, 1.8.
Using the exp algorithm from Weiss:
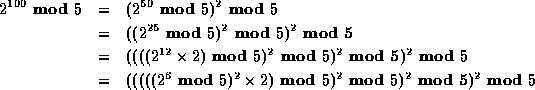
We could continue down to the base case of the algorithm, but
since we know 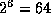 , we know that
, we know that 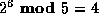 ,
and we can start plugging in the values:
,
and we can start plugging in the values:

Perhaps it is easier, as humans, to work from the bottom up
instead of from the top down (as the exp algorithm
does). For example:
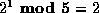 ,
,
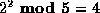 ,
,
 , etc.
, etc.
Since each further doubling of the exponent just
results in multiplying 1 by 1, there's no need to
continue this table:
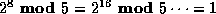 .
.
Noting that
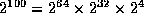 , we know that
, we know that
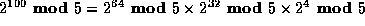 , which is 1.
, which is 1.
- (20 points) Weiss, 2.1.
 .
.
Keep in mind that we are interested in the rate of growth, not
the actual values of these functions. This is why 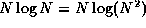 , even though
, even though 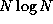 is generally smaller.
Recall that the logarithm of a product is the sum of the
logarithms of the factors (which anyone who has used a slide
rule knows well). Therefore,
is generally smaller.
Recall that the logarithm of a product is the sum of the
logarithms of the factors (which anyone who has used a slide
rule knows well). Therefore, 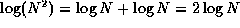 .
.
The case of 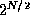 and
and 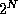 may appear similar, but is
actually different. Both grow at an exponential rate, but
may appear similar, but is
actually different. Both grow at an exponential rate, but
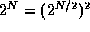 , so
, so 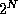 will always be larger by a
factor of
will always be larger by a
factor of 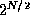 , and this factor grows larger as N
increases.
, and this factor grows larger as N
increases.
- (12 points) Weiss, 2.2.
- True.
- False. A counterexample comes directly from the course notes:
if
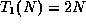 and
and 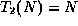 , then
, then
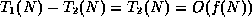 .
If f(N) = N, then
.
If f(N) = N, then 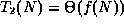 ,
but not o(f(N)).
,
but not o(f(N)).
- False. Recall that big-O notation is based on
an inequality: it gives a bound on the growth
rate, but that is all. This is almost a trick
question, because it is conventional to use
the smallest possible bound for the big-O, but
this is not required by the definition of big-O.
In this case, if we let 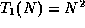 and
and 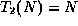 , and
, and 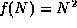 , then
it is true that
, then
it is true that 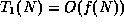 and
and
 , but
, but
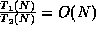 .
.
- False. Use the same
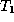 and
and 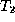 as in
the previous example.
as in
the previous example.
- (12 points) Weiss, 2.6.
O(N), 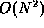 ,
, 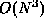 ,
, 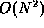 ,
,  ,
, 
- (5 points) Weiss, 2.20.
In general, arithmetic operations take more time to process
larger numbers. However, if we used a fixed integer size,
then there is a fixed bound on how large the operands to the
arithmetic operations can be. Therefore, there is a fixed
bound on how long each operation can possibly take, based on
this maximum size. Therefore, all arithmetic operations are
O(1).
- (5 points) What is an abstract data type? What is a data
structure? What is the difference? Give at least one example
of each.
An abstract data type is a set of operations defined over a
set of types. An abstract data type specifies what the
operations do, but not how the operations are accomplished.
A data structure is a means of representing data, generally in
a manner that makes the data easy to access or manipulate. A
data structure does define how the data is represented, but
does not define any operations on the data.
A list is an abstract data type. Linked lists, which are one
way to implement the list ADT, are a data structure.
- (15 points) Weiss, 3.5.
The most straightforward way is to duplicate the algorithm
from class for finding the intersection, but instead of only
adding to the output list when the keys are equal, always add
the item as it is hopped over, except when they are equal, in
which case only add one.
The following pseudo-code assumes a linked-list
representation, and assumes that the keys in each list are
unique (no duplicates in either list).
while (L1 != NULL && L2 != NULL) {
if (L1->key == L2->key) {
Add L1->key to union
L1 = Advance (L1);
L2 = Advance (L2);
}
else if (L1->key < L2->key) {
Add L1->key to union
L1 = Advance (L1);
}
else {
Add L2->key to union
L2 = Advance (L2);
}
}
/* Now deal with any leftovers: */
while (L1 != NULL) {
Add L1->key to union
L1 = Advance (L1);
}
while (L2 != NULL) {
Add L2->key to union
L2 = Advance (L2);
}
To handle duplicates properly, we can replace all of the calls
to Advance with calls to a function that advances to the
next element that has a different value than the current,
thereby skipping over all duplicates.
- (10 points) Weiss, 3.11.
- (10 points) Weiss, 3.17.
Advantage- speeds up groups of deletions. Since deletion in
a singly linked list is O(n), deleting a bunch of stuff can
be expensive. If we delete an entire list starting at the end
of moving forward, this can take 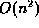 time! However, by
sweeping down the list and doing all the deletions at one, we
can clean up any number of lazily deleted nodes in a single
O(n) traversal. Therefore, if we have a lot of deletions to
perform, this can be much more efficient than deleting
elements one at a time.
time! However, by
sweeping down the list and doing all the deletions at one, we
can clean up any number of lazily deleted nodes in a single
O(n) traversal. Therefore, if we have a lot of deletions to
perform, this can be much more efficient than deleting
elements one at a time.
Disadvantage- slows down other operations. Since the list
may become cluttered with lazily deleted elements, it may take
longer to traverse the list to do a FIND or FindKth. (Note,
however, that since the number of lazily deleted elements is
always proportional to the number of elements in the list,
these operations are still O(n).) As a related disadvantage,
the memory consumed by these elements is unreclaimed, so our
program may use a lot more memory than necessary (at worst,
twice as much, because we won't scrub the list until half the
elements have been deleted).
- (10 points) Weiss, 3.21.
Have one stack grow up from the ``bottom'' of the array, while
the other grows down from the ``top''. They will only meet in
the middle when there is no more space whatsoever.
Programming this requires a little extra care to make sure
that not only are the stacks not running past the ends of the
arrays, but they're also not clobbering each other.
- (10 points) Weiss, 3.23.
- (5 points) Write an algorithm that searches for a key in an
binary search tree.
See lecture notes, or Weiss.
- (5 points) Write an algorithm that searches for a key in an
unordered binary tree.
This is more complicated. Because there is no order, we need
to search everywhere in the tree. Modifying a traversal
is the easiest way to accomplish this:
tree_t *treeFindUnordered (tree_t *t, int key)
{
tree_t *result;
if (t == NULL)
return (NULL);
else if (t->key == key)
return (t);
else if (result = treeFindUnordered (t->left, key) != NULL)
return (result);
else
return (treeFindUnordered (t->right, key));
}
- (15 points) Write an algorithm that determines whether
both keys A and B (where A < B) are present in a binary
search tree. In the worst case, this might take as much time
as searching for A and then searching again for B, but in
the best case you should be able to save a considerable
amount of time.
The best case is when A and B are ``near'' each other in
the tree. This depends entirely upon the tree and is
independent of A and B.
One method is to start a search for A, using the ordinary
algorithm, but also compare each key to B. If a node is
encountered where the decision of whether to go left or right
would be different for A and B, then split the search; do
an ordinary lookup for A to the left and for B to the
right.
If the search has not been split, and a match for A
is found, search the right descendants of this node for B.
If the search has not been split, and a match for B
is found, search the left descendants of this node for A.
Because A < B, at worst the search for A can eliminate the
nodes less than A from consideration during the search for
B.
For this kind of optimization, the true benefit is not usually
the reduction in comparisons needed (although this is never a
bad thing). The real benefit comes when the tree is
``difficult'' to traverse- for example, a database stored on
disk, where visiting each node requires a disk access.
- (10 points) Weiss 4.28.
- (10 points) Weiss 4.40. Similar to sparse arrays,
from the course book.
- (15 points) Weiss 4.42. (Assuming that the tree is binary,
and that the keys in each node are unique.)
Observations:
- If the roots of the two trees do not contain the same
keys, or have different numbers of children, then the
trees are not isomorphic.
- If the roots of two trees do contain the same keys, and
the left subtree of the first is isomorphic with the
left subtree of the second, and the right subtree is
isomorphic with the right child of the second, then
the trees are isomorphic, then the trees are
isomorphic.
- If the roots of two trees do contain the same keys, and
the left subtree of the first is isomorphic with the
right subtree of the second, and the right subtree is
isomorphic with the left child of the second, then the
trees are isomorphic.
- (15 points) Weiss 4.44.
One way to implement FindKth is simply to do an inorder
traversal, stopping at the Kth node. Unfortunately, this is
O(n), and we want something faster.
Another approach is that each node in the tree can keep track
of how many left descendants it has. If K is less than
the number of the roots left descendants, then the Kth element must
be a left descendant of the root; otherwise it is either the root or
a right descendant. This process of elimination can be repeated
recursively (or iteratively) until the correct node is found.
The complicated part is keeping this information up-to-date.
When Insert is used, the descendant count must be updated for
all of its ancestors. However, as we descend the tree, we
cannot increment the descendant counts, because we don't know
whether or not this is a new key or a duplicate- so the
updating must be done separately from the search.
The same is true for Delete; we must not update any descendant
counts until we know that something was actually removed.
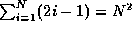 .
.
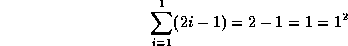
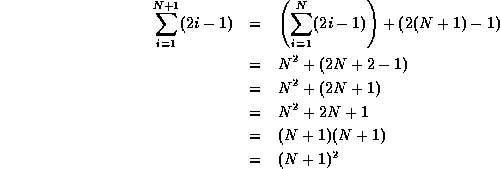
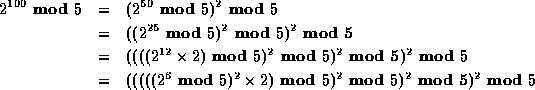
![]() , we know that
, we know that ![]() ,
and we can start plugging in the values:
,
and we can start plugging in the values:

![]() ,
,
![]() ,
,
![]() , etc.
, etc.
![]() .
.
![]() , we know that
, we know that
![]() , which is 1.
, which is 1.
![]() .
.
![]() , even though
, even though ![]() is generally smaller.
Recall that the logarithm of a product is the sum of the
logarithms of the factors (which anyone who has used a slide
rule knows well). Therefore,
is generally smaller.
Recall that the logarithm of a product is the sum of the
logarithms of the factors (which anyone who has used a slide
rule knows well). Therefore, ![]() .
.
![]() and
and ![]() may appear similar, but is
actually different. Both grow at an exponential rate, but
may appear similar, but is
actually different. Both grow at an exponential rate, but
![]() , so
, so ![]() will always be larger by a
factor of
will always be larger by a
factor of ![]() , and this factor grows larger as N
increases.
, and this factor grows larger as N
increases.
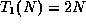 and
and 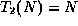 , then
, then
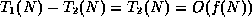 .
If f(N) = N, then
.
If f(N) = N, then 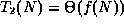 ,
but not o(f(N)).
,
but not o(f(N)).
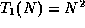 and
and 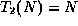 , and
, and 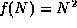 , then
it is true that
, then
it is true that 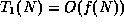 and
and
 , but
, but
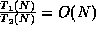 .
.
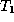 and
and 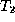 as in
the previous example.
as in
the previous example.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()