S-Q 1997 - Practice Final

This practice final is intended as a study aid for the 1997 S-Q final exam. There are many more problems here than will actually on the exam, so this is not meant to represent the same length of test as the exam. Each problem is assigned a point value that is roughly proportional to the number of minutes that I expect you would spend on that problem during the exam. (The same point scheme will be used on the actual exam.)

Some of the more difficult or general problems are not assignment point values.

In addition to these problems, working through the practice midterms is a good exercise. (Some of the questions here are reproduced from the practice midterms.)

Many of the questions here have answers that can be found in the book. The point is that you should be able, at this point, to answer these kinds of questions without looking in the book.

• The exam will be closed book and closed notes.
• Many of the problems are given with hints. On the exam, there will generally be fewer hints.
• The problems are divided into several categories; you should expect to find at least one problem from each category on the exam.
• The problems from the Weiss book are good review, but many are harder than what will be on the midterm.
• Some of the problems here are similar (or nearly identical) to some of the problems that you have seen in the reading or lecture. Make sure that you can work through them yourself, without looking at your notes!

Background

1. (10 minutes) What are big-O, big-Theta, and big-Omega? What is the difference between big-O and little-o?
2. (15 minutes) Prove that any polynomial over x of degree p is .

Lists, Stacks, and Queues

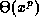Some of these questions are taken verbatim from the practice hourlies.

1. (5 minutes) What is an abstract data type? What is a data structure? What is the difference? Give at least one example of each.
2. (15 minutes) Weiss, 3.5. The notation 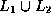means ``all the elements in 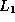or 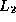'' (but only one instance of each- the result must have no duplicated values.)

   There is an algorithm that runs in O(n) time (where n is the length of the longest list) for linked lists (actually, a tighter bound can be placed on the running time if the lists are of unequal length). This is not unlike something we did in class.

Trees and Tries

1. (5 minutes) Starting with an empty tree, show the result of adding the following integer keys to a binary search tree:

   5 10 1 0 2 4 3 7 9

2. (10 minutes) Starting with an empty tree, show the result of adding the following integer keys to a binary search AVL tree:

   5 10 1 0 2 4 3 7 9

3. (5 minutes) Starting with an empty tree, show the result of adding the following integer keys to a 2-3 tree:

   5 10 1 0 2 4 3 7 9

4. (10 minutes) Show how any binary search tree can be constructed by a sequence of insertions. Show that this is not true for AVL or 2-3 trees.
5. (10 minutes) Insert the following keys into an initially empty trie. Show the resulting trie after each insertion.

   dog dogfish bland band bond fish

6. (10 minutes) Same as the previous problem, but assume that the underlying trie data structure is implemented by a de la Briandais tree.
7. (10 minutes) Insert the following keys into an empty patricia. Show the resulting patricia after each insertion.

   dog dogfish cat catfish cattle dogged

8. (10 minutes) Give an algorithm for deleting a key from a binary search tree. What are the special cases? Hint- try to combine special cases so that there are fewer to worry about.
9. (15 minutes) Give an algorithm for deleting a key from a trie. What are the special cases?
10. (15 minutes) Give an algorithm for deleting a key from a patricia. What are the special cases?

Hashing

1. (10 minutes) One possible hash function is the following: treat each character in the string as a number in the range 0..255. Compute the sum of all of the characters in the string, then take the result modulo the size of the hash function.

   Name at least two reasons why this is usually a poor hash function. Name at least one situation where it might be practical. Hint- consider the behavior of this hashing function in assignment 4.

2. (5 minutes) Discuss why the hash function from Kernighan and Ritchie (hash0 from assignment 4) works much better than the hash function from Weiss (hash1 from assignment 4).

Randomized Algorithms

1. (5 minutes) What is the difference between true randomness and pseudo-randomness?
2. (5 minutes) What is a randomized algorithm? Why would you ever want to use a randomized algorithm?
3. (5 minutes) What is a probabilistic algorithm? Why would you ever want to use a probabilistic algorithm?
4. (10 minutes) Describe the Monte Carlo method. Be specific, and give examples.
5. (10 minutes) Factorization is a problem that is believed to be very hard- given a number x that has only two large prime factors, a and b, finding a and b rapidly is very difficult.
   1. Assuming that factorization is hard, show how to construct a brown envelope capable of keeping a single large prime secret until it is opened. You may assume that generating random, large primes (which may be helpful) is fast and easy to accomplish.
   2. Show how the recipient of the brown envelope can verify the secret, once it has been revealed.

Sorting

1. (5 minutes) Briefly state the bubblesort algorithm.
2. (5 minutes) Briefly state the selectionsort algorithm.
3. (5 minutes) Briefly state the insertionsort algorithm.
4. (8 minutes) Briefly state the quicksort algorithm.
5. (8 minutes) Briefly state the mergesort algorithm.
6. (8 minutes) Briefly state the heapsort algorithm. What is the relationship between heapsort and selectionsort?
7. (5 minutes) Briefly state the bucketsort algorithm. What kinds of keys can be sorted with bucketsort?
8. (5 minutes) What is the difference between ``normal'' bucketsort and the stable bucketsort, in terms of implementation? When is each appropriate?
9. (8 minutes) Briefly state the radixsort algorithm. What kinds of keys can be sorted with radixsort?
10. (10 minutes) Briefly explain the importance of choosing a good pivot in quicksort. Describe what can happen if poor pivots are chosen. Describe three different ways of choosing pivots, and access their likelihood of choosing well.
11. (10 minutes) Show the process of bubble-sorting the following array. Show each comparison and swap that takes place.

    5 3 9 4 0 1 8

12. (5 minutes) Show the process of selection-sorting the following array. Show each comparison and swap that takes place.

    5 3 9 4 0 1 8

13. (5 minutes) Show the process of insertion-sorting the following array. Show each comparison and swap that takes place.

    5 3 9 4 0 1 8

14. (5 minutes) Show the process of quick-sorting the following array. Use the first element in each partition as the pivot (so 5 is the first pivot, for example). Show the array after each partitioning step.

    5 3 9 4 0 1 8

15. (5 minutes) Show the process of merge-sorting the following array. Show the array before each merge and after the final merge.

    5 3 9 4 0 1 8

16. (20 minutes) Mergesort was described recursively in lecture. Describe how it can be implemented iteratively, using looping constructs. (Do not ``simulate'' the recursive algorithm by using a stack.)

    Hint- one approach is similar, in some regards, to the outer loop of the O(N) heapify algorithm. (However, this hint may be more confusing than clarifying...)

17. Explain why any sorting algorithm that compares and exchanges only adjacent array elements must be 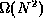in the worst case. (This is straight out of the notes, but make sure you can explain this without your notes!)
18. Explain why any sorting algorithm that exchanges only adjacent array elements (but can compare distant elements) must still be 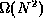in the worst case. (If you understand the answer to the last problem, the answer to this problem should be immediate.)
19. (10-20 minutes each) For each of the following sorting algorithms, prove whether or not they are stable (assuming that the algorithms presented in class and/or the book are used).
    • Bubble sort.
    • Selection sort.
    • Insertion sort.
    • Merge sort.
    • Quick sort.

20. For each of the sorts in the previous problem that you proved was not stable, describe how to change their algorithm (in some reasonably small way) to make them stable.
21. It is somewhat harder to analyze whether heapsort is stable. Determine whether it is. Show a counterexample if it is not, and briefly describe why.

Heaps

1. (10 minutes) Build a heap by inserting the following integer keys to an intially empty MIN heap (i.e. a heap where the root is always the minimum key). Show the resulting heap after each insertion:

   1 10 4 5 3 7 8 12 0

2. (5 minutes) Show the result of performing five DeleteMin operations on the heap that was produced by the previous question. Show the resulting heap after each deletion.
3. (8 minutes) Build a MIN heap using the Heapify operation on the following array of integer keys:

   8 9 7 4 5 1 0 2 3

4. (23 minutes) Repeat the previous three questions, but use a MAX heap (i.e. a heap where the root is always the maximum key) instead of a MIN heap.
5. (15 minutes) Show the resulting array after each step of heapsorting the following array of integers:

   5 2 3 8 1 7 4 9

6. (20 minutes) A collegue of yours doesn't believe that the DeleteMin algorithm (for a MIN heap) actually works- they don't believe that the result has the heap order property. Prove that it does. Draw diagrams, if appropriate.
7. (15 minutes) Your same collegue is now skeptical about whether Insert works. Prove that it does.

Graphs

There will be questions about graphs on the final exam, but until I see how far we get in lecture this week, I won't know how much to ask.

About this document ...

This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 fin_prac.tex.

The translation was initiated by Dan Ellard on Wed Aug 6 10:43:06 EDT 1997