S-Q 1997 - Assignment 5
Due 08/07/97 at 6:00pm
Last Date Accepted: 08/11/97 at 6:00pm
- Copy over the files for this assignment. Copy all of the files
from
libsq/assts/asst5 into your directory
/Q/asst5 (which should have been
created when you ran q-setup for
assignment 1).
All work should be done in directory /Q/asst5. The
Makefile provided includes rules to build all the programs in this
assignment; you shouldn't need to change it at all.
You may write your answers to the written questions in whatever manner
you prefer- longhand, with UNIX tools, or via a word processor. Make
sure to hand in a copy of whatever is appropriate given your choice.
- (5 points) Weiss, 6.13. Give a precise equation, in terms of
d and i. Hint- test your equation for d = 2 and make
sure that it gives the same answer as for binary heaps, and
then test it for larger d. Remember that the first element
of the array is at index 0.
- (20 points) Weiss, 6.2, part b only. Initially fill the tree in
level order with the given values (so that 10 is the root, 12
its left child, 1 its right child, and so on) and then show
each step of the procedure.
- (25 points) Alice and Bob agree to play the following game:
Alice will randomly select a 50-digit binary number, and
conceal it from Bob. Bob will then attempt to guess the
number. Since Alice has
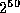possible numbers to choose
from, Alice has agreed to make Bob's task easier by allowing
Bob to ask her, as often as he likes, one very specific
question: Bob can ask Alice whether a given string of bits
appears as a substring in her number. For example, Bob might
ask if ``1010'' appears in the Alice's number, and she would
answer yes if and only if this pattern of binary digits
appears somewhere in her number.
To end the game, Bob declares his final guess, and Alice
reveals her number. If Bob's guess is correct, then Bob wins,
but if his guess is incorrect, then Alice wins. Note that Bob
must commit to one (and only one) number as his final guess.
Hint- this problem has much more to do with string searching
than brown envelopes.
- Show that Bob can always win this game after asking a
relatively small number of questions (i.e. fewer than
500). Calculate the minimum and maximum number of
questions that Bob will require to always win if he
uses your algorithm.
- Alice can attempt to cheat by showing Bob a number that
is different than the one she initially chose, or by
answering some of Bob's questions incorrectly. Prove
that any attempt by Alice to cheat can easily be
detected by Bob, as soon as she reveals her number.
- (30 points) Implement the radix sorting algorithm for integers,
by completing the functions in file radixsort.c.
- (20 points) Weiss, 6.9, part a. Remember that your goal is not
to find the K smallest numbers- your goal is simply to find
all the numbers smaller than X. You need only FIND the nodes
in question -- you do NOT need to delete them from the heap.
(Note that it is possible that none of the numbers in the heap is
smaller then X, or it is possible that they all are.)
An undirected graph is minimally connected if it is connected,
but the removal of any edge would cause the graph to become
disconnected.
- Prove that any minimally connected graph which contains N nodes
must contain exactly N-1 edges.
- Devise an efficient (O(N)) algorithm for determining whether
an undirected graph is minimally connected. If possible,
prove that your algorithm is O(N) in all cases. If your
algorithm is not O(N), state what its big-O is (and prove
this bound).
For the purpose of this algorithm, you can assume that given a
vertex X, you can find a list of all of the vertices
adjacent to X in time O(1).
- Implement your algorithm, using the code provided in mincon.c.
- Use the submit program to hand in your work. From
your directory /Q, run the submit
program. The name of the course is cscisq, and the
name of the project is asst5, and the name of the file
to submit is also asst5. (See the UNIX tutorial for
more info about submit.)
- Print out a copy of all of the text or code files you created or
edited as part of this assignment,
and hand them in at the
next class or section.
If you wrote out the
answers to your questions longhand or using a word processor,
include printouts of the final document.
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 asst5.tex.
The translation was initiated by Dan Ellard on Wed Jul 30 11:41:01 EDT 1997
Dan Ellard
Wed Jul 30 11:41:01 EDT 1997