S-Q 1997 - Assignment 1
Due 06/30/97 at 6:00pm
Last Date Accepted: 07/03/97 at 6:00pm
This assignment is intended to familiarize you with the computers that
we'll be using in this course and to help me assess your current knowledge
of C and programming, as well as to reinforce the concepts that we've covered
in lecture and reading so far.
The first three problems are short programming exercises. They should
be straightforward if you are comfortable with C, recursion, and strings
(though array_middle is somewhat more difficult than the others).
The last two problems are much more thought-provoking.
- Set up your account for S-Q work. Run the command
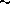/libsq/usr/scripts/q-setup, which will create a number
of directories that you will use for your assignments, and
configure your account for S-Q work (by adding a few lines to
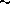your /.cshrc).
If you get any warning messages when you run q-setup, please
send mail to the course staff. After you've run
q-setup, log out and log back in again, and your
environment should be set up. (You should not need to repeat
this step.)
NOTE: if you're not running tcsh or csh, then you should talk
to a member of the course staff about how to set up your
account environment. (If you are not sure what shell you are
running, then you're probably running tcsh.)
- Copy over the files for this assignment. Copy all of
the files from 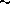libsq/assts/asst1 into your directory
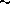/Q/asst1. (This directory is created by
q-setup, so you don't need to create it yourself.)
All work should be done in directory 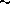/Q/asst1.
- (25 points) Implement functions array_max,
array_first, array_last, and
array_middle, as described in array.c. Use
program array_test to test your functions. (The
Makefile we provide includes a definition for
array_test, so in your asst1 directory the
command make array_test will compile this program.)
- (15 points) Implement functions string_append and
string_substr, as described in string.c. Use
program string_test to test your functions. (The
Makefile we provide includes a definition for
string_test, so in your asst1 directory the
command make string_test will compile this program.)
- (15 points) Weiss, problem 2.16. Write your algorithm in C, and
use it to implement function exp_iterative in file
exp.c. Use program exp_test to test your
exp_iterative function. (The Makefile we
provide includes a definition for exp_test, so in
your asst1 directory the command make exp_test
will compile this program.)
- (25 points) Weiss, problem 2.19, parts a, b, c, and d. Write
your answer in majority.txt. A few hints:
- Make sure that you understand why and how the candidate
selection algorithm works before you attempt to solve
part b.
- There are several approaches to part d. Be sure to
state what assumptions, if any, you need to make in
order for your approach to work.
- (20 points) Suppose that you have an array A that contains N
integers, and you need to devise an algorithm that takes two
numbers x and y (where
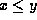), and computes the sum of all
of the integers in A between index x and index y. For
example, if A is 10, 2, 4, 5, 1, -4, 0, 4 , then if x is 2
and y is 5, the sum is A[2] + A[3] + A[4] + A[5] = 4 + 5 + 1 -
4 = 6.
Imagine that it is very important that this algorithm run
quickly, but that you can perform any amount of precomputation
(before you discover x and y). One approach would be to
compute the answers for every possible x and y ahead of time,
keeping the answers in an N by N array. When given an x and
y, you can find the sum immediately in this array. This
algorithm runs in time O(1) (not counting the precomputation),
but requires space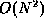 
, so for a large N this
approach is impractical. Luckily, algorithms exist that are
nearly as fast, but use much less memory.
Answer the following questions in sum.txt:
- Find an algorithm that runs in time O(1) (not counting
any necessary precomputation) but uses only O(N)
precomputed values. Express your algorithm (including
the precomputation) in clear English and/or
pseudo-code.
- Discuss the tradeoff between memory usage and speed. It
is possible to compute the sum in y-x arithmetic operations
using no precomputed results, or with one
arithmetic operation using N precomputed values. How
many arithmetic operations are necessary to compute the
sum, in general, if you can only store N/2 precomputed
values? N/4? N/8? N/M (where M < N)?
- Use the submit program to hand in your work. From your
directory 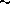/Q, run the submit program. The
name of the course is cscisq, and the name of the
project is asst1, and the name of the file to submit is
also asst1. (See the UNIX tutorial for more info about
submit.)
- Print out a copy of files array.c, exp.c, string.c,
majority.txt, and sum.txt, and hand them in during the next
class or section.
This document was generated using the LaTeX2HTML translator Version 96.1-h (September 30, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 asst1.tex.
The translation was initiated by Dan Ellard on Fri Jun 27 16:02:56 EDT 1997
Dan Ellard
Fri Jun 27 16:02:56 EDT 1997